

Development of Astronomy in Ottomans

Generally, it is possible to study the development of astronomy in the Ottomans in three periods; The astronomy from the establishment of Ottomans to Ali Qushji’s arrival in the Ottomans (1299-1472); The astronomy from Ali Qushji’s arrival in Ottomans to the demolition of Istanbul Observatory (1472-1580) and The astronomy after the demolition of Istanbul Observatory......
Generally, it is possible to study the development of astronomy in the Ottomans in three periods;
- The astronomy from the establishment of Ottomans to Ali Qushji’s arrival in the Ottomans (1299-1472)
- The astronomy from Ali Qushji’s arrival in Ottomans to the demolition of Istanbul Observatory (1472-1580)
- The astronomy after the demolition of Istanbul Observatory
 Figure 1. Part of the manuscript which shows Istanbul Observatory
Figure 1. Part of the manuscript which shows Istanbul Observatory(Source: Ottoman Contributions to Science and Technology by Salim Ayduz)
In the first period, it cannot be said that the astronomical studies were productive just like the other scientific areas. There is only one scientist who stands out in this period, Ahmad-i Dâî, who is famous with Risâla-i Sî Fasıl (The Treatise in Thirty Chapters) which consists of translations of al-Muhtasar fî Ilm al-Tancîm va Marifat al-Takvîm (Summary of the Astronomy and Calendars) by Nasîrüddin al-Tûsî. In addition to this book, there are a few books about cosmology and cosmogony. Generally, these books include the basis for Ptolemaic astronomy.
The second period begins with Ali Qushji’s arrival in Istanbul. He was educated in Semerqand by Ulugh Beg and was directed to Semerqand Observatory which was founded in 1421 by Ulugh Beg. After Ulugh Beg’s death, he came to Istanbul in 1472 by the insistence of Mehmet II.

Figure 2. Artistic impression of Ali Al-Qushji (Source: Ali Al-Qushji… by Ilay Ileri )
Ali Qushji was born in Samarkand. The last name Qushji derived from the Turkish term kuşçu – the falconer – due to the fact that Ali’s father Muhammad was the royal falconer of Ulugh Beg. He took courses in the linguistic sciences, mathematics, and astronomy as well as other sciences taught by scholars in the circle of Ulugh Beg. In 1420, Qushji secretly moved to Kirman where he studied the mathematical sciences. Upon his return to Samarqand, he presented Ulugh Beg with a monograph (Ḥall eshkāl al‐muʿaddil li‐l‐masīr) (Explanations of the Equation of Mercury) in which he solved the problems related to Mercury.
Ulugh Beg was fascinated with the works and read the entire work while standing up. Ulugh Beg assigned him to Samarkand Observatory at that time. He worked there till Ulugh Beg was assassinated.

Figure 3. Statue of Ulugh Beg and his students, Registan square, Samarqand, Uzbekistan (Source: Ulugh Beg” )
After Ulugh Beg’s death, Ali Qushji went to Herat, Tashkent and finally Tabriz. The Ak Koyunlu ruler Uzun Hasan sent him as a delegate to the Ottoman Sultan Mehmed II. When Qūshjī and his entourage approached Istanbul, Sultan Mehmed sent a group of scholars to welcome them. Upon arrival in Istanbul, Qūshjī presented his mathematical work entitled al‐Muḥammadiyya fī al‐ḥisāb and his astronomical works entitled al-Fathiyya to the Sultan.
Qūshjī spent the remaining two years of his life in Istanbul. He educated and influenced a large number of students, who, along with his writings were to have an enormous impact on future generations. He was buried in the cemetery of the Eyyūb mosque.
Qushji improved on Nasir al-Din al-Tusi’s planetary model and presented an alternative planetary model for Mercury. He was also one of the astronomers that were part of Ulugh Beg‘s team of researchers working at the Samarqand observatory and contributed towards the Zij-i-Sultani compiled there.
Whereas he died in 1474 in Istanbul, Ottomans mathematics and astronomies raised by him, because he educated a few students so that important astronomers grown up after him. One of them is Taqî al-Dîn. He studied optics, mathematics, astronomy, and mechanics. Istanbul Observatory was established by him in 1575. But it was demolished in 1580 and after that Ottomans science was stroked. He made lots of precise astronomical instruments, applied the clocks into astronomy and used trigonometrically functions in astronomy and might have been used a telescope.

Figure 4. 1001 Inventions book, Astrolobe section in Astronomy zone, Page 280-821
(Source: Star-finders Astrolabes by Cem Nizamoglu)
Taqî al Dîn al Râsid
Taqî al Dîn al Râsıd (Taqî al Dîn Mehmed ibn Maruf al Hanafi al Dımışkî) was one of the greatest 16th-century Ottoman scholars. He was born in Damascus in 1526 and studied both there and in Egypt. In 1550 he came to Istanbul with his father Marûf Efendi, and in 1555 went to Egypt, where he served as a member of the judiciary. He returned to Istanbul in 1570, and a year later, upon the death of chief astrologer Mustafa Çelebi, was appointed to this post by Sultan Selim II. While serving in this position he began making astronomical observations from Galata Tower, and in 1577 was authorized by Sultan Murad III to build a new observatory on the hillside above Tophane on the shore of the Bosphorus. Regrettably, this observatory was demolished in 1580 after the chief religious functionary in the Ottoman Empire issued a decree alleging that countries possessing observatories were struck by disasters. Taqî al Dîn died five years later in 1585.
Taqî al Dîn carried out research not only in mathematics and astronomy but optics and medicine. His work on the subject of trigonometry is particularly notable. Although the renowned 16th-century astronomer Copernicus (1473-1543) did not use the sine function, or even mention sines, cosines, tangents, and cotangents, Taqî al Dîn defined all of these, gave their proofs, and drew up tables. Moreover, he began to use decimal fractions in place of the sixtieth fractions that had long been used by mathematicians.
Taqî al Dîn was also a skilled technician, who built sundials and mechanical clocks, and designed various machines for raising water from lakes, rivers, and wells, giving detailed accounts of these in one of his books.
Of his numerous works on astronomy, optics, mathematics and mechanics, the best-known and most widely researched arc the following:
- Bugyat al-Tüllâb min İlm al-Hisâb (What We Expect of Arithmetic)
- Sidret al-Muntahâ al-Efkâr fî Malak al-Falak al-Davvâr (Frontier of Knowledge of the Skies)
- Tashîl Zîj al-A ‘sariyya al- Sbahinshâhiya (Interpretation of Tables Based on the Decimal System of the Sultan)
- Caridat al-Durar ve Harida al-Fikar (Compilation of Pearls and the Finest of Ideas)
- Al-Turuk al-Saniya fî al-Âlat al-Rûhâniya (Outstanding Methods for Automatons), 1385.
- Al-Kavâkih al-Duriyafî Bangâmât al-Davriya (Brightest Stars Concerning the Construction of Mechanical Clocks), 1556.
A work by another author, probably one of the astronomers who worked with Taqî al Dîn, describes the astronomical instruments used at Taqî al Dîn’s observatory in Istanbul. Entitled Âlât al-Rasadîya li Zîj-i Şahinshâhîya (The Astronomical Instruments for the Royal Astronomical Tables), it was written in Turkish between 1575 and 1577.

Figure 5. The overview of the astronomical instruments and staff of the Istanbul Observatory with Taqi Al-Din Rasid at work from Shahinshahnāme, (Book of the Shah of the Shahs), 1581 (Source: A Chronology – Turkey’s 700-year… by Feza Günergun)
Istanbul Observatory
Taqî al Dîn’s observatory established in Istanbul in the second half of the 16th century was the first to be built in the Ottoman Empire, and so has an important place in Ottoman scientific history.
When he arrived in Istanbul in 1570, Taqî al Dîn immediately got in touch with the foremost scholars of the time, encouraging their interest in the idea of establishing an observatory. Vezir Sokullu Mehmed Pasha and royal chronicler Hoca Saadettin, with whom Taqî al Dîn became friendly while serving as chief astrologer, lent their support to the project. Taqî al Dîn wrote a report explaining that the astronomical tables of Central Asian Turkish astronomer and ruler Ulugh Bey were now out of date and unable meet the needs of the time; and therefore those new observations were necessary in order to draw up new tables. Hoca Saadettin and Sokullu Mehmed Pasha presented this report to Sultan Murad III. And they persuaded him that an observatory should be established under the direction of Taqî al Dîn. The subject was presented to the Council of State and endorsed. Murad III’s interest in astrology and desire to see into the future were an important factor in his approval of the project. In 1575 Taqî al Dîn was charged with preparing an astronomical manual in the name of the sultan. Although sources disagree on the exact dates, scholars generally concur in thinking that construction of the observatory began in 1575 and was completed in 1577.
The Observatory Building
We do not know exactly how large the observatory was, although we know that it included offices and sleeping accommodation for both astronomers and administrative staff, and a library. Next to the main building was another described in historical sources as the Small Observatory, which is perhaps where the portable astronomical instruments were kept.
Some sources record that the observatory included an observation shaft (either underground in the form of a well or above ground in the form of a tower). Its existence was popularly believed and became associated in time with an earlier celebrated astronomer, Ali Kuşçu (d. 1474). In fact, modern scholars have come to the conclusion that Istanbul Observatory did not possess such a shaft, although Taqî al Dîn is said to have used one while he was in Cairo.
The names and duties of some of those employed at the observatory are preserved in archive documents, and fifteen people worked under Taqî al Dîn, including the second and third astronomers, a clerk and an assistant.
In November 1577 the celebrated comet which was seen right across the northern hemisphere appeared in the sky over Istanbul. In his capacity as a royal astrologer, Taqî al Dîn made predictions to Sultan Murad based on the appearance of the comet, interpreting it as a favorable sign, and prophesying a Turkish victory over the Iranians. However, when a plague epidemic struck the city in 1578, public hostility to the observatory spread rapidly, and certain quarters at court took advantage of this opportunity to allege that every country where an observatory was established was beset by a succession of catastrophes, citing Ulugh Bey as an example. Sheikh ul-lslam Kadızâde Ahmed Shemseddin Efendi wrote a report to the sultan, asserting that astronomical observation was ill-omened; that those who had the audacity to attempt to lift the curtain of mystery from the spheres would suffer the consequences; and that a country where astronomical tables were drawn up would fail into ruins and its public buildings be destroyed by earthquake. The report had the desired effect, and an imperial rescript was sent to High Admiral Kılıç Ali Pasha commanding him to demolish the observatory. Almost certainly Taqî al Dîn only got away with his life due to the intervention of his friend and patron at court, Hoca Saadettin Efendi.

Figure 7. Remains of Jaipur observatory in India built by Maharajah Jai Singh in 1726. Early observations were carried out by the naked eye from the top of this monumental architectural structures. The monuments include a massive sundial, the Samrat Yantra, and a gnomon inclined at 27m , showing the altitude of Jaipur and the height of Pole Star. There is also a large astronomical sextant and a meridian chamber.
(Source: Astronomical Observatories in the Classical Islamic Culture by Salah Zaimeche)
Instruments Used at the Observatory
Istanbul Observatory was equipped with the most advanced instruments of the period, including two not known in Europe. Studies have shown that the other instruments were the same as those at the observatory established in 1576 in Hveen by the celebrated astronomer Tycho Brahe (1546-1601), under the patronage of King Frederick II of Denmark.

Figure 8. Ottoman Astronomer (Source)
Taqî al Dîn made astronomical instruments for the observatory. The following instruments were used at the observatory:
- Armillary sphere (dhât al-halâk)
- Mural quadrant (libne)
- Azimuthal semicircle (dhât al-samt va’l-irtifâ)
- Turquetum (dhât al-subatayn)
- Wooden quadrant (rûb-i mıstara)
- Dioptra (dhât al-sakbeteyn)
- Dhât al-Awtar
- Mushabbaha bil-Manâtiq
- Calibration Rule (sindî jatvali)
- Clock
Armillary sphere (dhât al-halâk)
For centuries this instrument, which was used to measure the latitude and longitude of heavenly bodies, was the foremost piece of equipment used by astronomers. The earliest known picture of this instrument appears in Ptolemy’s Almagest (ca. 150 CE), where it is described as an astrolabe. The armillary sphere used by Taqî al Dîn was made of six hoops with a diameter of over 4 metres, and was suspended inside a horizon ring, which was underpinned by six columns upon a base. Armillary spheres used in 16th century Europe were similarly constructed.
Mural quadrant (libne)
This type of quadrant was fixed to the surface of a vertical wall standing on a meridian plane. It was used to observe the culmination of celestial bodies, that is, the point at which they cross the meridian. As the name implies a quadrant consists of a quarter circles. Ptolemy discussed the astronomical use of the quadrant in detail, and instruments of the type he described were subsequently used in the Islamic world from an early period. The first Islamic author to write about the quadrant was Harezmî in the 9th century. The mural quadrant at Istanbul Observatory was 6 metres in diameter.
Azimuthal semicircle (dhhât al-samt va’l-irtifâ)

Figure 9. Sextant of Tycho Brahe (Source: Astronomical Instruments of Tycho Brahe and Taqi al-Din)
This instrument—the forerunner of the theodolite—was used to calculate the height of heavenly bodies and their azimuth, and had been used in the Islamic world since the time of Ibn Sina(980-1037). Naşir al Dîn al Tûsî (1201-1274) perfected its design. It was first used in Europe by Tycho Brahe.
Taqî al Dîn’s azimuthal semicircle consists of a vertical semicircle 1.5 meters in diameter balanced at the centre of a horizon ring.
Turquetum (dhhât al-subatayn)
The earliest known illustration of this instrument, also known as a parallactic ruler, is by Ptolemy, and that used by Taqî al Dîn is precisely the same. Fixed to the meridian plane, it was used for measuring the height of heavenly bodies from any angle.
Wooden Quadrant (rûb-i mistara)
A quadrant made of wooden rulers used for measuring the height and zenith of stars. Tycho Brahe and Taqî al Dîn appear to have been the first astronomers to ever use this instrument. That at Taqî al Dîn’s observatory had a radius of 4.5 metres.
Dioptra (dhât al-sakbeteyn)
Also known in English as alidade, this instrument consisting of a ruler with two sights was used for measuring the diameter of the sun and moon, and eclipses. Taqî al Dîn’s dioptra was so large that it could even show the minutes.
Dbât al-Awtar
This instrument for calculating the equinox was invented by Taqî al Dîn. In his explanation of an illustration of instruments in one of his works, he says that it replaces the earlier solar armillary used for the same purpose.
Mushabbaha bil-Manâtiq
This resembled a sextant, and was used for measuring angles between two heavenly bodies in any plane. It was one of the most important 16th century inventions of practical astronomy. It consisted of three graduated arcs, and was used for measuring the sides of a spherical triangle formed by three stars. Taqî al Dîn says that this instrument was his own invention.
Calibration Rule (sindî catvali)
Also known as the suneydî ruler, this was a calibration rule used to increase the precision of instruments.
Clock
The clock is classified as an astronomical instrument in Âlât al-Rasadiya and Sidrat al-Muntabâ. The most important characteristics of astronomical clocks were their accuracy and ability to precisely measure minutes and seconds. In Europe time was first divided into minutes and seconds in 1550. In his al-Kavâkib al-Duriya written in 1556, Taqî al Dîn speaks of the division of hours into minutes.
The right ascensions of the stars are measured as the angular distance between the sun and the stars and calculated by means of the time that passes. This requires accurate clocks, but it was not until the second half of the 16th century that clocks became sufficiently accurate to be useful to astronomers. Tycho Brahe constructed three clocks for this purpose, and Taqî al Dîn also used astronomical clocks in his observatory. In Âlât al-Rasadiya the author quotes Ptolemy as saying, ‘If I could measure time precisely, I could do without observation altogether.’ In the section on instruments in Sidrat al-Muntahâ, Taqî al Dîn says that Ptolemy had not found a method even to measure minutes, never mind degrees and that therefore he had been forced to abandon the search for precision. By means of his astronomical clock, Taqî al Dîn says that he had fulfilled Ptolemy’s ambition.
This clock designed and made by Taqî al Dîn is a kind of mechanical clock. As we learn from Sidret al-Müntehâ it comprises three separate trains of cogwheels, each turning three hands or pointers located on a large sphere. The force which drives each is a large weight attached to a short rope. The pointers are on separate dials, one showing the number of hours, another angle of the sun in degrees, and another the minutes. The interval between each mark on the minute dial, which was divided into 360, represented 10 seconds, and by having this, it was possible to measure time to an accuracy of 5 seconds.

Figures 10-11. In the middle part of this famous manuscript of an Istanbul observatory (left) is a clock placed on a table that is believed to be Taqi al-Din’s. Computer animated rendering of the workings of Taqī al-Dīn’s observational clock is shown on the right. © FSTC Ltd.
(Source: Ingenious Clocks from Muslim Civilisation… by Cem Nizamoglu)
Astronomical Clocks
Astronomical clocks show the movement of the celestial bodies. The first example is the mechanical clock built between 1348 and 1362 by the Italian Giovanni Jacobo de Dondi. This clock showed the movements of five planets, the sun and the moon. Another astronomical clock built by Eberhard Baldewin in 1561 showed the positions of the stars as well as the planets, sun and moon.
In his al-Kavâkib al-Duriya Taqî al Dîn describes how such clocks are made and their seven types, the sixth of which is his own invention. They showed the days of the month and week, the phases of the moon, the position of the sun on the ecliptic, the positions of the moon and sun relative to one another, the azimuths of some of the fixed stars, their right ascensions and altitudes, and the times of prayer.
Taqî al Dîn says the following on the subject of constructing an astronomical clock that will show prayer times:
Then in the year 971 [1561], I was faced with the problem of making a clock which would tell the times of prayer. So I made a dial and marked it with the necessary times, which were the temcid, dawn, Friday. mid-fasting, morning, afternoon, evening, bedtime and midnight prayers. By means of another dial it is possible to tell the degree of the sun and the first day of the months in the Julian calendar.
Again in the same work, Taqî al Dîn gives an account of making wall and table clocks. He was clearly aware of the types of table clocks being made in 16th century Europe, and refers to those with double compartments, single compartments, and horizontal mechanisms. He gives particularly detailed information about striking movements.
Taqî al Dîn describes pocket clocks’ in al-Kavâkib al-Duriya: ‘The pallets taper towards the inside, so that the surface of each becomes equal to the radius of the cylinder. Some people make them circular in form, and some leave them as they are in pocket clocks.’ He goes on to write that a cogwheel that revolves once in every degree can show minutes and other values.
In other books that he wrote between 1575 and 1576, he refers to a clock showing the seconds, minutes and hours that he made for using at Istanbul Observatory.

Figure 12. City of Istanbul and Develi illumination from Matrakçi’s Beyân-i Menâzil-i Sefer-i ‘Irakeyn(Source: “Maps from Muslim Civilisation“ by Cem Nizamoglu and Khaleel Shaikh)
Did Taqî al Dîn Use a Telescope?
Another piece of equipment which Taqî al Dîn seems to have used is an optical instrument which made things far off appear nearer. In his Kitâb Nur Hadakat al-Ebsâr ve Nur Hadîkat al-Enzâr (Book on the Light of the Gardens of the Eye and Vision) he writes:
‘I made a crystal [lens] similar to that which the Greek scholars made and placed in the tower at Alexandria, and which, when we look through it with one eye, is capable of showing in the smallest detail objects which are so far away that they are invisible, and the sails of ships in the middle distance.’
According to known sources, the first telescope was made in the 1600s, and the first astronomical telescope by Galileo (1564-1642) in 1609. Yet Taqî al Dîn was writing at the beginning of 1574. The instrument Taqî al Dîn describes perhaps cannot be described as a telescope as such, but may have been a proto-telescope of the type known as a ‘sighting tube’. Another interesting point about his account is that the Lighthouse at Alexandria is not recorded in any other source as possessing an instrument of the kind Taqî al Dîn describes.
Astronomical Observations Made by Taqî al Dîn
Our knowledge of the observations made at the observatory in Istanbul is based on three zîj or manuals of astronomical tables written by Taqî al Dîn:
- Sidrat al-Muntahâ (1577/78-1580)
- Tashîl Zîj al-A’sariya al-Shâhinshâhiya (1580)
- Carîdat al-Durar (1584)
In Sidrat al-Muntabâ Taqî al Dîn mentions observations of the sun in 1577 and 1579 for the purpose of calculating Istanbul’s latitude. In this manual, there are no lunar tables, which are given in Tasbîl Zîj al-A ‘sariya and Carîdat al-Durar. The latter two manuals give tables of latitude for the planets Saturn, Venus and Mercury, and tables of lunar eclipses. Carîdat al-Durar also includes a table drawn up in 1581 giving the positions of 69 stars. His calculations concerning the theory of solar motion based on astronomical observations are regarded as the most outstanding work of its kind in the world in the 16th century.
The last period of Ottomans astronomy starts with the demolishment of the Istanbul Observatory. The astronomy in Ottomans was not developed after this. After 17th century, Ottomans has tried to follow the new science developed in the west and met the Copernican astronomy. However, the new astronomy wasn’t accepted till the beginnings of the 19th century and a new observatory named Rasathane-i Âmire was established in 1867.
The first contacts of the Ottoman Turks with the modern astronomy which developed in the axis of Nicolaus Copernicus (d. 1543), Tycho Brahe (d. 1601), Galilei Galileo (d. 1642), Johannes Kepler (d. 1630) and Isaac Newton (d.1727) had begun in the middle of the 17th century. The first works that provided the introduction of the modern astronomy to Ottomans were generally the translations of astronomical tables and geography studies. These contacts about the new astronomy had continued with the translations of West geography works in the 18th century and with the translations of French astronomical tables in the second half of the 18th century.

Figure 14. Portrait of Copernicus (beginning of the 16th century). (Source: Copernicus and Arabic Astronomy by George Saliba )
The first work that mentioned the Copernican System was the translation of the astronomical table (Novae Motuum Caelestium Ephemerides Richelianae, 1637) of the French astronomer Noel Durret (d. 1650) with the name in the Ottoman Turkish language Sajanjal al-Aflāk fi Ghāyat al-idrāk (The Mirror of the Heaven in a Quite Perception) between the years 1660-1664, by Ibrahim Efendi al-Zigetvari Tezkireci (the end of the 17th century) who was Zigetvar originated and settled in Istanbul. Ibrahim Efendi mentioned the tables written up to that date and then about the astronomical table of Copernicus.
As far as we know it is the first book that was transferred from the European languages about astronomical tables. Ibrahim Efendi, translated Durret’s table into Arabic first, then with the encouragement of Kazasker Unsi Efendi (d. 1664) he translated it into Turkish.
The second work that had mentioned the modern astronomy was the Nusrat al-Islām va‘l-Surūr fi Tahrīri Atlas Mayor (1685) which was a reduction of the Latin work shortly known as Atlas Major. It was prepared by Abū Bakr ibn Bahrām ibn Abdullāh al-Hanafi al-Dimashki (d. 1692) who was one of the 17th-century Ottoman geographers and he was known as Geographer Abu Bakr Efendi.
Dimashki was charged with the translation of the book prepared by Wilhelm Blaue (d. 1638) and his son Joan which was completed in 1662 and was published in 1664 in Amsterdam as ten volumes, named Atlas Major (seu Cosmographia Blaeuiana Qua Solum, Coelum Accuratissime Describuntur) because of his knowledge on mathematics, geography and Latin by the Sultan Mehmet the IV.
In 1968, a copy of this work was represented to the sultan by the ambassador of Holland, Justin Colier and this work was translated by Dimashki with the name Nusrat al-Islām va‘l-Surūr fi Tahrīri Atlas Mayor as six volumes between the years 1675 and 1685. Dimashki had not only translated the work he also had added some information about the Ottoman geography. And also after a while, he published a summary of the work called as Muhtasar Nusrat al-Islām va‘l-Surūr.
The work that comes after these two works is the Cihannüma edition of Müteferrika. The additions of Müteferrika to the Katip Chelebi’s Cihannüma have the feature of being the largest writing that provided the new astronomy subjects to be known in the Ottoman culture in real. After printing Cihannüma a year later with this addition, Müteferrika, translated the astronomy work of Andreas Cellarius’ (d. 1665) Atlas Coelestics, which was first published in 1660 in Latin by the order of the Ahmed the 3rd with the name of “Macmūa Hay’a al-Kadīme va‘l-Cadīda (The New and Old Astronomy Magazine, 1733) and by the way an independent work about the new and old astronomy had been acquired to the Ottoman Science.
 Figure 15. A page from Kâtib Çelebi’s Kitâb-i Cihânnümâ / Jihân-numâ (Cosmorama), Istanbul: Ibrahim Müteferrika, 1732.
Figure 15. A page from Kâtib Çelebi’s Kitâb-i Cihânnümâ / Jihân-numâ (Cosmorama), Istanbul: Ibrahim Müteferrika, 1732.(Source: Manuscripts and printing in the spread of Muslim science by Geoffrey Roper)
Another new work about the new astronomy subject is Tarcuma-i Kitāb-i Cografya (The Translation of Geography Book, 1751) by Osman ibn Abdulmannān. Osman ibn Abdulmannan (d. 1786’s) is probably Bosnian originated. During the governorship of Köprülü Hacı Ahmet Pasha (d. 1769) in Belgrad, he worked as the second interpreter of this city’s council of state. He began to translate the important works of European languages with the encouragement of Hacı Ahmet Pasha beginning by the year 1749. Between the years 1749-1791, he translated Bernhard Varenius’ (d. 1676), the Holland doctor, physician and geographer, Geographia Generalis (in Qua Affectionnes Generalles Telluris Explicantur) (1650) from German into Turkish as Tarcuma-i Kitāb-ı Cografya.
By the various translations of the tables, it is seen that the Ottoman astronomers were following the Western Astronomy studies. In the seventeenth century, after the translation of French astronomer Noel Durret’s table by Ibrahim Efendi, Kalfazade Ismail Çınari have translated Alexis Claude Claraut’s table in 1767 and Jacques Cassini’s table in 1772. Later on, by the order of Selim the III the calendars have begun to be arranged according to this table and by the time the Zīc-i Ulugh Bey which had been used since then, have been left.
Tarcuma-i Zīc-i Klaro (Translation of Clariaut’s Table) is a translation of the book Theorie de la Lune published in 1752 of Alexis- Claude Clairaut (d. 1765) from French. The book was translated in 1767 and it was dedicated to Sultan Mustafa the third.
The second book that was translated by Ismail Efendi is Jacques Cassini’ (d. 1756) Tables Astronomiques de Soleil (de la Lune, des Planetes, de Etoiles Fixes et des Satellites de Jupiter et de Saturne) (Paris, 1740) called as Tuhfa-i Bahīc-i Rasīni Tarcuma-i Zīc-i Kasīnī (The Translation of Cassini’s Tables) in 1772 from French.
Another work about Copernicus Astronomy is Erzurumlu Ibrahim Hakkı’s Mārifetnāme which was completed in 1757 and was first published in 1825. In this work three sources were used for explaining the comprehension of the Universe, and the solar and lunar eclipses and the natural events; 1) the religious sources, including the Holy Koran, the hadiths and religious sources 2) the scientific works like Katip Çelebi’s Cihannüma with the additions of Müteferrika) the folk beliefs like Suyuti’s work including the legends and superstitions.

Figure 16. Erzurumlu İbrahim Hakkı published an explanation of the Solar Eclipse in his encyclopedia Marifetname
(Source: Nearly 3 Centuries old light system… by Cem Nizamoglu)
Tarcuma-i Zīc-i Laland (The Translation of Lalande’s Table) translated by Hüseyin Hüsnī ibn Ahmed Sabīh (d. 1840) which was written by Joseph-Jeome Lefrançais de Lalande was one of the translations of tables mentioning the new astronomy. Hüseyin Hüsnī ibn Ahmed Sabīh had lived in Istanbul in the 19th century and he became the chief Astrologer of the Ottoman Sultan. First he had been to the Arabic countries and then he came to Istanbul. He became the second astrolog at Mahmut the II period and after the death of Mehmet Rakım Efendi in 1825 he was assigned as the chief astrolog of the Sultan. Then he became the Kadhi of Selanik in1838 and he died in 1839 (or 1840).
Tarcuma-i Zīc-i Laland is the translation of Joseph-Jeome Lefrançais de Lalande’s (d. 1807) Tables Astronomiques (Paris 1759). Hüseyin hüsni translated this book first into Arabic in 1814 then into Turkish in 1826. Tarcuma-i Zīc-i Laland is the Turkish translation of the book Tables Astronomiques’ making a calender part’s broadened version in six sections. In the preface, it is told that the table of Lalande was prepared according to the Copernican System and invalidated the Ulugh Bey and Cassini’s Tables and this new table would be valid till the Doomsday.
Besides the translations of the West astronomy sources, it is seen that for the first time the Copernican astronomy had been mentioned in a work which was prepared by using a Russian source. This book is the translation of Agha ibn Mirzā Muhammed Han-ı Sanī of Abasku’s (d. 1846), known as Kudsī of Baku, book with the name of Asrār al-Malakūt (The Mystery of Angels). Kudsī of Baku translated the book first into Persian then into Arabic and he presented it to the Sultan in 1846. The book took the Sultan’s attention and it was translated into Turkish by Hayatizade Seyyid Sherif Halil al-Albistani with the name of Afkār al-Cabarrūt fi Tarcama Asrār al-Malakūt with the order of Reshid Pasha in 1848.
At the late eighteenth century, these studies show us that the Ottomans began to have contacts with the West not only in geography but also in astronomy and in mathematics fields at least the theoretical information that was needed in the first plan. However, the Ottomans translated the tables which were involving the information about how to identify the time. Although there were lots of works that changed the structure of the astronomy in the West, choosing that kind of tables showed the general dominant character of Ottomans about science in that era.
(Source: International Women’s Day by Cem Nizamoglu)
Astronomy began to be taught by the state itself after the foundation of Mühendishāne-i Bahrī-i Humāyun (The School of Naval Engineering) in 1773 and Mühendishāne-i Berrī-i Humāyun (The school of Ground Forces Engineering) in 1793. Hüseyin Rıfkı Tāmāni (d. 1817), who was the first principal of the Mühendishāne-i Berrī- Humāyun which was founded in the Sultan Selim the III’s time, had great efforts in the arrangement of the lessons in Mühendishāne, and also he was one of the pioneers to divert the contemporary West science to the Ottomans by the help of his knowledge of English, French, Italian and Latin besides Arabic and Persian.
Hüseyin Rıfkı Tāmāni was the first teacher that gave lessons on astronomy in Mühendishāne-i Berrī-i Humāyun. Hüseyin Rıfkı Tāmāni did not have an independent book related to the astronomy. One of his students; Hodja Ishak Efendi summarised his notes about the geography and published as al-Madhāl fi’l-Cografya (An Introduction to the Geography) in 1831. The astronomy system given here in this book is the Earth-centered System. On the other hand, in Hüseyin Rıfkı’s work Macmūa al-Muhandisīn (The Magazine of the Engineers) which was about the contemporary physic; the measurement of the meridian circle was given. According to him to measure one degreed meridian is important from two aspects; by the way, an international unity would be able to do in order to find the unit of measurement and the real shape of the Earth would be defined. Finally, as a result of the measurement, the shape of the Earth was proved to be protruding on the Equator and compressed at the poles as Newton projected.
Seyyid Ali Pasha became the principal after Hüseyin Rıfkı Tamani in Mühendishāne-i Berrī-i Humāyun in 1817. Seyyid Ali Pasha translated Ali Qushi’s, who was one of the important astronomers of the fifteenth century, al-Fathiyya with the name of Mirāt-ı al-ālam (The Mirror of the Universe) and in the preface he mentioned about the existence of three approaches in the astronomy. These are; Ptolemaios’ Earth-centered system, Pythagoras’ and Copernicus’ Sun-centered System and Brahe’s system that puts both the Sun and the Earth in the center. Seyyid Ali Pasha said that the Earth-centered system was common in the Islamic countries, the tables prepared to arrange calendars were depending on this system and by the way it had been accepted.
In 1830 Ishak Efendi was assigned as the principal after the dismissal of Seyyid Ali Pasha. Ishak Efendi saved his most important work; Macmūa-i ‘Ulūm-i Riyāziya’s fourth volume to the astronomy and mostly the Theory of Copernicus and gave the longest and probably the most technical description of this system in Ottomans “although it is possible to be mistaken” absolutely defined that the approach of Copernicus was most proper to the science.
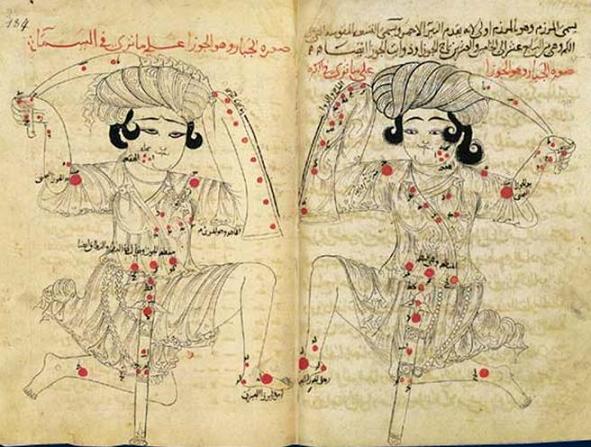
Figure 18. The depiction of Orion, as seen from Earth (left) and a mirror-image, from a 13th-century copy of al-Sufi’s Book of the Fixed Stars. In this version, Orion’s shield has become a long sleeve, typical of Islamic dress.
(Source: “Arabic Star Names…” by Zakri Abdul Hamid)
Bibliography
- Kaçar, Mustafa, M. Şinasi Acar & Atilla Bir, XVI. Yüzyıl Osmanlı Astronomu Takiyüddin’in Gözlem Araçları, Istanbul 2011.
- Tekeli, Sevim, “İstanbul Rasathanesinin Gözlem Araçları,” Araştırma, Cilt 11, 1979, s. 29-44.
- Tekeli, Sevim, “Meçhul Bir Yazarın İstanbul Rasathanesinin Âletlerinin Tasvirini Veren ‘Âlât-ı Rasadiye li Zîc-i Şehinşâhiye Adlı Makalesi”, Araştırma, Cilt 1, 1963, s. 71-122.
- Tekeli, Sevim, “Nasîrüddin, Takiyüddin ve Tycho Brahe’nin Rasat Aletlerinin Mukayesesi”, Ankara Üniversitesi, Dil ve Tarih-Coğrafya Fakültesi Dergisi, Cilt 16, Sayı 3-4, 1958, s. 301-393.
- Unat, Yavuz, “Time in The Sky of Istanbul, Taqî al Dîn al-Râsid’s Observatory”, Art and Culture Magazine, Time in Art, Winter 2004/Issue 11, pp.86–103.
- Unat, Yavuz, “The Ottoman Astronomy in General”, The Ottoman, vol., 8, Edited by Güler Eren, Ankara 1999, s. 411-420.
- Unat, Yavuz, Tarih Boyunca Türklerde Gökbilim, (Astronomy in Turks), Istanbul 2008.
- Unat, Yavuz, Ali Kuşçu, Istanbul 2009.
“Development of Astronomy in Ottomans”
by Prof. Dr. Yavuz Unat, Kastamonu University
3rd Azarquiel School of Astronomy, A Bridge Between East and West, July 8-15, 2012, İstanbul Kültür Üniversitesi, İstanbul 2012.
by Prof. Dr. Yavuz Unat, Kastamonu University
3rd Azarquiel School of Astronomy, A Bridge Between East and West, July 8-15, 2012, İstanbul Kültür Üniversitesi, İstanbul 2012.






















No hay comentarios:
Publicar un comentario